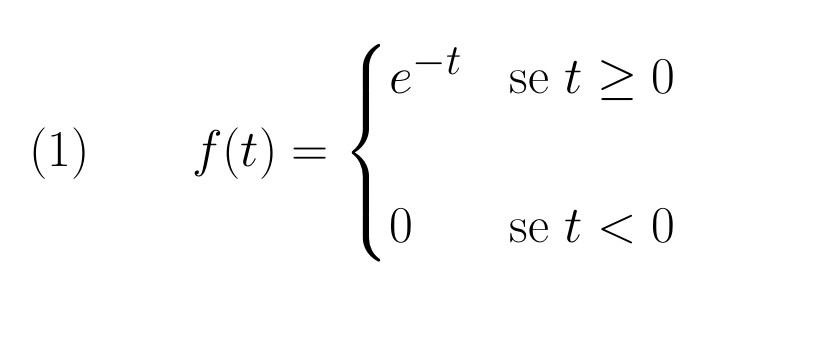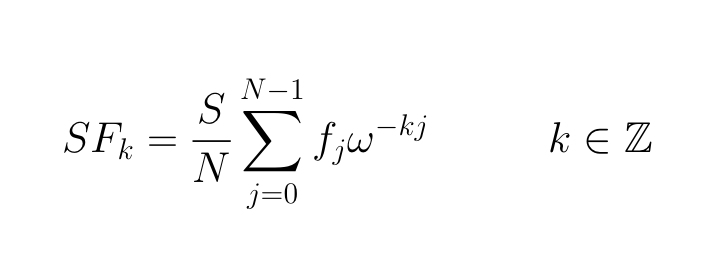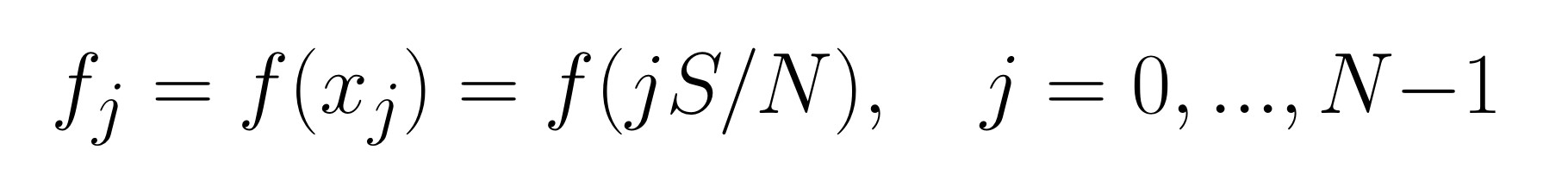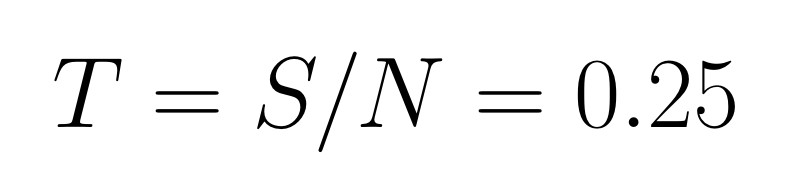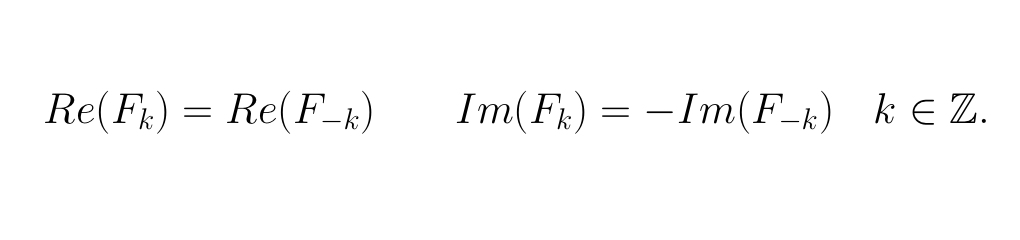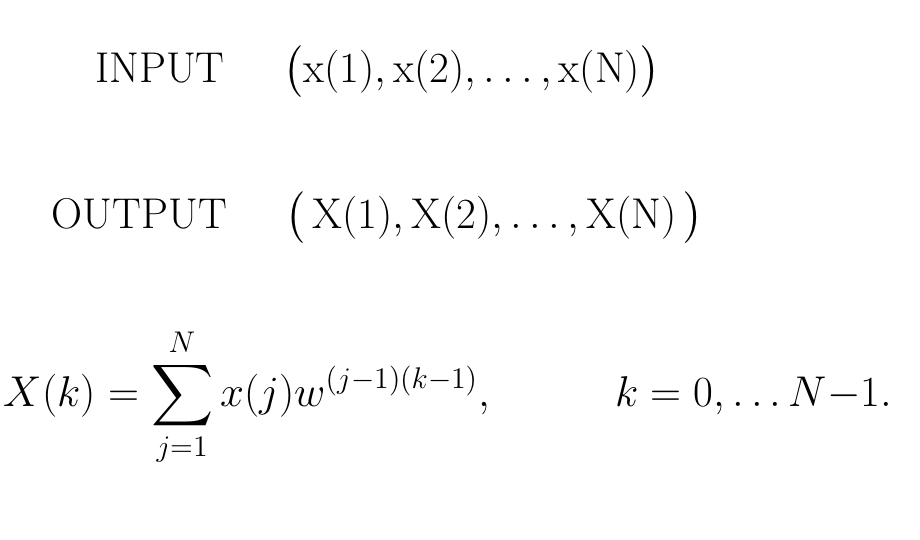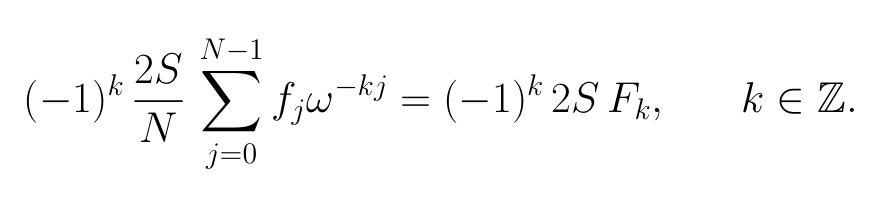4.11.2014

CALCOLO NUMERICO DELLA TRASFORMATA DI FOURIER DI UNA FUNZIONE  REALE: UN  ESEMPIO 

PRIMA PARTE

Per seguire agevolmente questo tutorial è necessario conoscere   

• le Sezioni 1, 2, 3 del Capitolo 3
• la Sezione 7 del Capitolo 3,  in particolare  le  Osservazioni 1-5, pag 133 -134.

 e aver fatto  gli Esercizi 4.1 e 4.3   pag 132

Alla fine di questa esposizione si dovrebbe essere in grado di svolgere i seguenti esercizi assegnati

Esercizi 5.0, 5.1, 5.2 a pagina 134

Illustriamo la tecnica per il calcolo numerico della trasformata di Fourier di una funzione attraverso un esperimento proposto da E. O. Brigham in The Fast Fourier Transform, Prentice Hall Englewood Cliffs, Boston, 1974.

Esperimento: data la funzione

si vuole calcolare numericamente la sua trasformata di Fourier di f  e confrontare con la trasformata vera:
quest'ultima  si può  calcolare esplicitamente, ed è: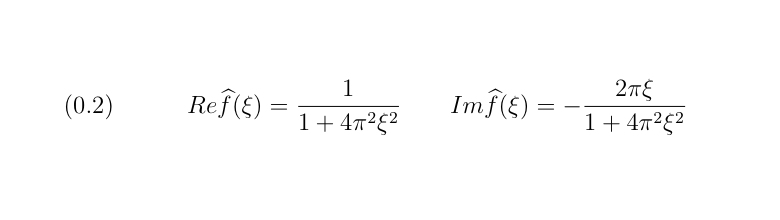

 

Si noti: la parte reale è pari e la parte immaginaria è dispari, perchè  f  è reale (Esercizio 3.3).

Calcoleremo la trasformata della sua restrizione all'intervallo [0,8] (perciò il parametro S delle note è  S=8).
In queste pagine continueremo a denotare  con  f  tale restrizione.

Sia N=32 il numero di punti scelto per calcolare la DFT; l'approssimazione di f^ è



dove

e la spaziatura fra i campioni  è

Conviene qui ricordare che     è una successione N-periodica.

Si noti: come accade per  la trasformata continua, la parte reale della DFT è pari, la parte immaginaria è dispari  (vedi Esercizio 4.3 pag 128):

Seguendo il  suggerimento dell'autore, useremo l'accortezza di modificare nell'origine la funzione assegnata, ponendola uguale a 0.5 invece che a 1. Rimandiamo per il momento la discussione sulle motivazioni di questa scelta (vedi Osservazione in fondo a questa pagina).

Scrittura del programma. Il programma esegue i seguenti passi

•  PASSO 1    Campionare la funzione: siano le campionature

  

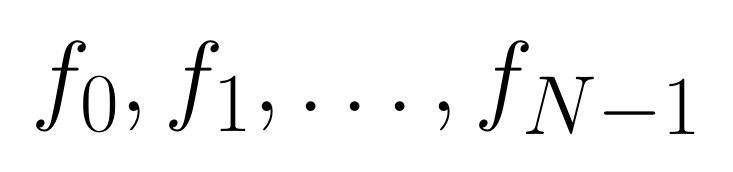
• PASSO 2    Applicare  la routine del Matlab con nome  fft.m  per calcolare la DFT di questa N-pla.  Questo programma prende in input gli N valori della funzione f campionata e ne restituisce  la  DFT 
  
                                                                  Moltiplichiamo per S e sia:                                                                                            
  

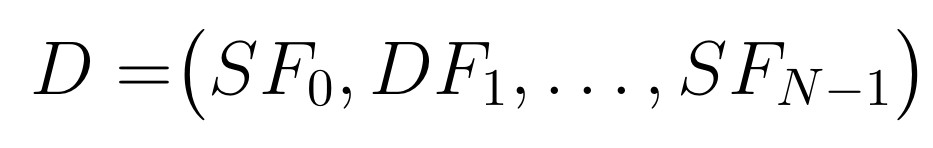
• PASSO 3   Separare la parte reale di D dalla parte immaginaria, ottenendo  

• PASSO 4    Interpretare quanto ottenuto. Confrontare  la trasformata calcolata con la vera, cioè                                      
  

                                                                               

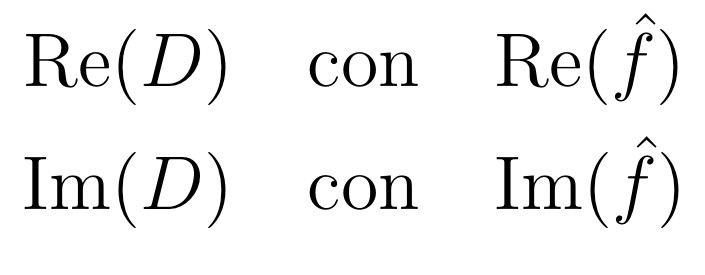
Infine sovrapporre i grafici.

Fine  del programma. 

 2- Calcolo della parte reale della trasformata.

Qui mostriamo cosa dovreste ottenere dopo i primi tre passi. In  Figura 1a compare il grafico dei campioni di f



FIGURA 1a. Punti di campionatura di f.  

Eseguiti i primi tre passi  del programma, avremo ottenuto  la N-pla
   
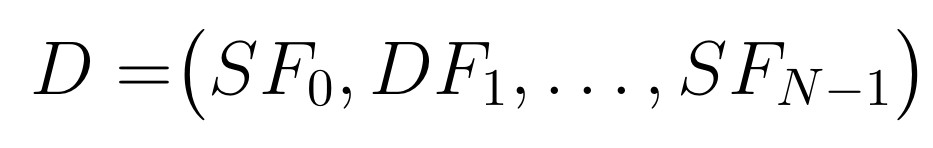
e  provveduto a separarne  la parte reale dalla parte immaginaria.     
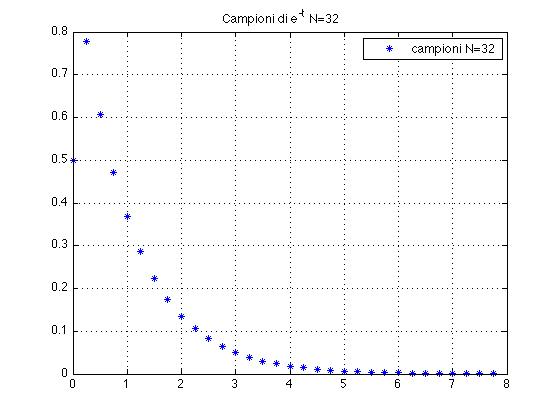
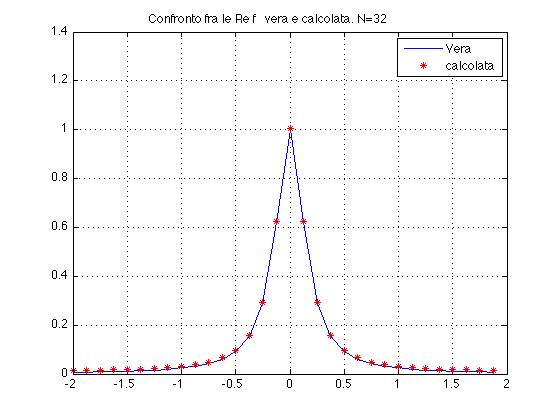
 Le Figure 2 e 3  qui sotto mostrano i grafici di Re(f^) e di Re(D)

  

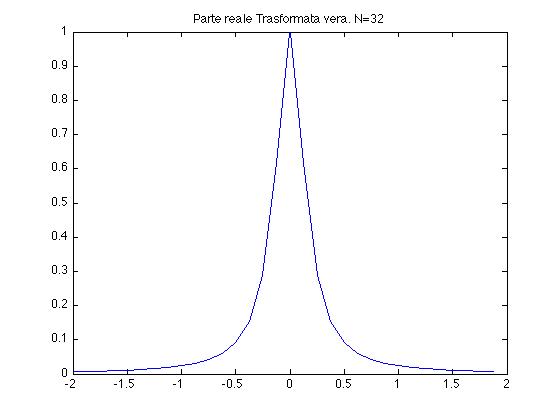
Figura 2 [a sinistra] Parte reale  della trasformata vera  in [-2,2]         
Figura 3 [a destra]   Plot della parte reale dell'output, punti (k,Re(SFk))  k=1,2,3,...N.

Intrpretazione dell'output  e confronto della trasformata vera con la calcolata.
La trasformata calcolata ad un primo esame può sembrare incorretta! Ma non è così: ricordiamo che la DFT è N-periodica;
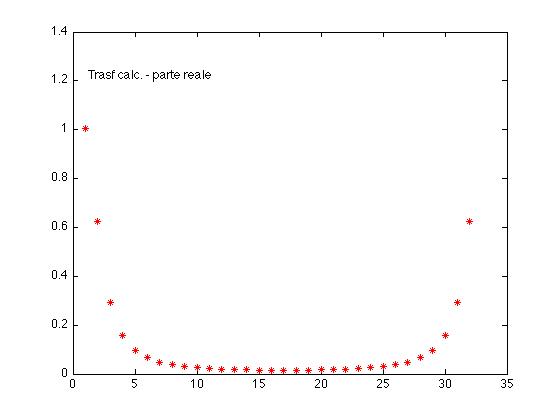
possiamo  visualizzare questa periodicità con il seguente grafico, avente in ascissa sempre numeri interi.



                                            k=0                                          k=N-1

Figura 3bis  Tre intervalli di periodicità della successione N-periodica Re(D) (che è pari)

Guardando la trasformata vera (Figura 2), si intuisce che il grafico della N-pla calcolata (in Figura 3bis qui sopra) è quello relativo all'intervallo [-N/2, N/2-1] (cioè l'intervallo, sugli interi, di ampiezza N e simmetrico rispetto a  k=0).
In Figura 4 si trovano i due grafici calcolata e vera sovrapposti.
Ci sarà utile in seguito l'osservazione che il grafico della calcolata si può ottenere da D ( Figura 3) traslando 
la seconda metà della N-pla a sinistra di zero della quantità  N/2:



Figura 4  Trasformata di Fourier calcolata  (puntini) e trasformata vera (linea continua) in [-2,2].


Osservazione. In questo caso la conoscenza della trasformata vera ci ha guidato nel tracciare il grafico della calcolata; in generale però la trasformata vera non è nota.
Si pone dunque la questione: quali valori  di  (f^)  rappresenta la N-pla trovata D?
In altri termini: in quale intervallo dell'asse delle frequenze  dobbiamo "collocare"
D per rappresentare graficamente la  f^ calcolata?
La risposta ci viene data dalla formula che esprime  la DFT in termini della trasformata vera (vedi  formule (1.8), (1.9), (1.10) pag. 112):

 

Dalla (0.1) si deduce che la spaziatura da prendere sull'asse delle frequenze per rappresentare graficamente la trasformata

calcolata  è 1/S,  e  l'intervallo deve avere ampiezza N/S, quindi sarà  [-N/2S,N/2S).

Dalla (0.1) si deduce che, se f^ è concentrata in [-N/2S, N/2S], allora D=(SF_k  k=0,..., N-1) è una buona approssimazione di f^  in questo intervallo perchè, fuori di esso, le "code" delle traslate sono trascurabili.

Inoltre

•  SF_0 (la media dei campioni moltiplicata per S)  approssima  f^(0) (la media  di f moltiplicata per S ) e  quindi  questi due punti dei due grafici vera-calcolata vanno sovrapposti    
  

• la prima metà della N-pla  Re(D)  approssima i valori di Re( f^) relativi alle frequenze positive:
  

            

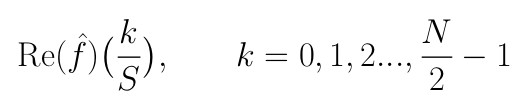
•  per la periodicità, la seconda metà della N-pla D approssima i valori di Re( f^) relativi alle frequenze negative
  

              

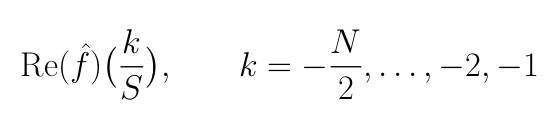
Quindi se vogliamo sovrapporre i grafici delle trasformate vera e calcolata, bisogna  prima fare uno "shift" della seconda metà di D portandola a sinistra dell'origine e poi sovrapporre questo grafico al grafico di Re( f^)(k/S),  k=-N/2,...  .., N/2-1 .

Nell'esempio in studio si ha [-N/2S, N/2S] =[-2,2] e i punti k/S sono k/8, k=-16, .....15.   (vedi Figura 4).

 Riassumendo, abbiamo campionato la funzione f in (1) nell'intervallo [0,8] con N=32 punti e ottenuto N valori della sua trasformata di Fourier  nell'intervallo [-N/2S, N/2S] =[-2,2].
Questi due intervalli, uno nel dominio dei tempi e l'altro nel dominio delle frequenze non vanno confusi.   

ESERCIZIO Ripetere l'esperimento con N=64  ed S (ancora) uguale a 8.
In questo caso i valori trovati saranno approssimazioni dei valori di f^  nell'intervallo  [-N/2S,N/2S)= [-4,4]
Si dovrà fare il plot di  f^ su tale intervallo valutandola in  N punti con spaziatura 1/8.
Sovrapporre il grafico della vera al grafico di D (dopo aver operato lo shift su D).
Questa questione sarà ancora discussa al punto 2 della  parte 3 più avanti.

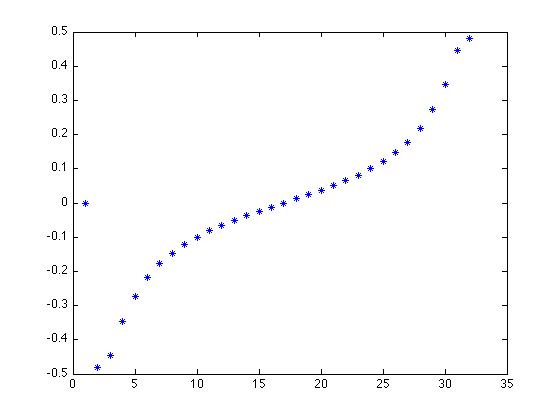
 2- Calcolo della parte immaginaria della trasformata.
 
Ripetendo le stesse operazioni per  la parte immaginaria della
trasformata si ottiene la N-pla riportata in Figura 5a)
 

Figura 5a) Parte immaginaria della trasformata calcolata, sull'asse  
delle ascisse compaiono i numeri naturali da 1 a 32.  

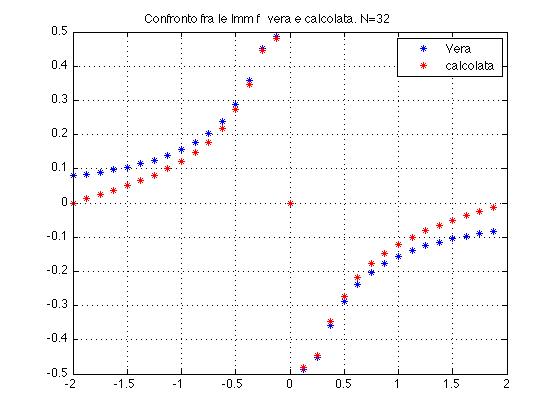
5 b) Parte immaginaria della trasformata di Fourier vera (puntini blu) e della

 calcolata (rossi).  L'intevallo sull'asse delle ascisse è [-2,2]. Notare l'errore al bordo.

 

Fatti  importanti per la  scrittura del programma  1 ) La  routine di Matlab  fft(x).m    esegue  il calcolo della somma qui sotto quindi bisogna successivamente moltiplicare per 1/N (e poi per l'ampiezza S dell'intervallo, ovviamente).  2.)  Per fare lo shift  di cui abbiamo parlato esiste una routine predisposta,  si chiama fftshift.m   Se  N=2M   è la dimensione del vettore H =(x_1,x_2,....,x_(2M)) , scrivendo  H1 =fftshift(H)   si ottiene H1=(x_(M+1), x_(M+2),...., x_(N), x_1, x_2,..., x_M) 3.) Se la funzione  f  da trasformare  è definita  su un intervallo [-R,S] allora bisogna usare la formula (1.11) delle note, che qui non riportiamo.  Se R=S la formula diventa  [cfr formula (1.12) delle note]. L'approssimazione di f^ in quest'ultimo caso è quindi la  (F_k) va moltiplicata, oltre che per l'ampiezza del supporto di  f,  anche  per (-1)^k ESERCIZIO Eseguire l'esperimento su esposto sulla parte immaginaria. Ripetere con N=64 come fatto per la parte reale.

 

SECONDA PARTE 1) Esiste una  routine per fare la trasformata inversa, si chiama ifft.m. Come abbiamo detto in 1) più sopra, il fattore 1/N non compare nella definizione di DFT; ma compare nella formula che  fornisce la trasformata inversa (in  ifft.m , controllare su help). Questo è naturale (ricordare la formula di inversione (2.3) pag 116 delle note.    2) Nel precedente esperimento la funzione da trasformare era reale. Se è complessa in generale, la parte  reale e la parte immaginaria della trasformata non sono nè pari nè dispari (verificare questa affermazione).  Lo stesso accade per la DFT ( verificare). In questi casi  l'individuazione dell'intervallo nel dominio delle frequenze in cui "collocare la N-pla trovata" non è così scontata. L'esercizio seguente illustra questo punto. Esercizio Per illustrare questo punto, i più esperti possono fare il percorso inverso  dell'esercizio  su esposto: assegnata f^ = Re(f^) +i Im(f^) in (0.2) calcolare  numericamente la funzione  f in (1). Consiglio di scrivere un  programma nuovo ripetto al precedente, iniziando con la scelta dell'intervallo su cui restringere la funzione  f^  e del numero di punti N  di campionatura. Raccomando molto questo esperimento, davvero istruttivo. Si noti che anche in  questo caso sappiamo già il risultato (conosciamo  la   f che è la  funzione (1) e quindi sappiamo "dove collocare" la  (SF_k) in un grafico (vale a dire scoprire a quali  valori delle ascisse corrispondono questi valori trovati), ma si pensi ad una situazione in cui questa è  sconosciuta, che è la tipica situazione reale!   Il seguente esercizio mostra che, assegnata una N-pla (f_o,....f_N-1),  ci sono più funzioni che hanno la stessa sua  DFT.  Questo mostra che in generale la conoscenza della DFT di una campionatura di una funzione f  consente di individuare valori di  f^ a meno di una traslazione.

 

 

 

TERZA  PARTE: CONTROLLO  DELL'ERRORE Vogliamo ora valutare le  fonti di errore nel calcolo numerico della trasformata di Fourier.  Per uno studio completo  si può  consultare il libro di W. L.  Briggs,  V. E.  Henson "The DFT". Non discuteremo l'errore dovuto al troncamento della funzione. Analizzeremo invece l'errore cosiddetto di aliasing.   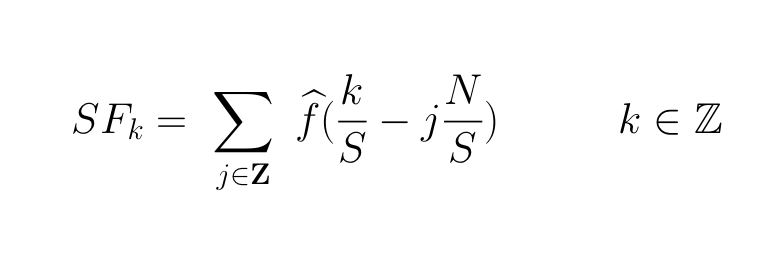Errore di Aliasing Abbiamo visto che se  f  ha supporto in  [0,S], SF_k  è uguale a   Dunque  si ha un errore di aliasing, che, come già sappiamo, tipicamente si manifesta ai bordi. Per ridurre questo errore si può rendere più grande il parametro del periodo N/S; così facendo  le code che "entrano"      in un intervallo  di periodicità saranno più piccole (ovviamente questo accade se f^  decresce all'infinito). Vale a dire, poichè S è fissato, si può prendere un numero N di punti più grande.  Quindi, per ridurre l'errore di aliasing,  bisogna prendere più punti di campionatura. Queste osservazioni sono particolarmente utili per l'Esercizio 5.3, che  ha proprio lo scopo di evidenziare questi errori. Considerazioni del tutto simili valgono nel caso f abbia supporto in un intervallo [-R,S], R e S>0.  OSSERVAZIONE (Sulla scelta di modificare la funzione assegnata nel punto t=0 ponendo f(0)=1/2).  Questa scelta corrisponde ad usare la regola dei trapezi al posto della regola  dei rettangoli nel calcolo  dell'integrale che esprime la trasformata di Fourier di f (in realtà anche l'estremo destro dell'intevallo  andrebbe  moltiplicato per 1/2, ma il valore della funzione in questo punto è piccolo).  Sappiamo che l'errore nella regola dei trapezi è più  piccolo di quello  nella regola dei rettangoli.    Conviene comunque sperimentare in entrambi i casi, sia operando questa correzione sia lasciando il  valore 1 in zero. Conviene verificare l'effetto della correzione sia sulla parte reale che sulla parte  immaginaria della calcolata. ASSEGNO DI ESERCIZI DI LABORATORIO: consegnare anche questi esperimenti.