La formula di Taylor 

A lezione avete visto che se f  è una funzione derivabile n volte in un punto x_0, allora per il  

Teorema di Taylor+Peano f(x) è uguale a 

= 

Questo fatto significa che f  e il suo polinomio di Taylor di grado n centrato in x_0 hanno contatto di ordine n. Al crescere di n, il contatto in x_0 aumenta, ovvero il grafico di f  e quello del suo polinomio di Taylor di grado n centrato in x_0 si assomigliano sempre di piu` in un intorno di x_0. 

Vediamo inizialmente come ricavare con Maple i polinomi di Taylor. 

>

restart;

 

>	taylor(exp(x),x=0,5);

 

(1)

 

Come vedete dalla risposta, il comando taylor(espress, x=x_0, n) vi fornisce lo SVILUPPO di Taylor
centrato in x_0 di ordine n-1. Il resto e` in forma O grande.  Siccome il risultato e` uno sviluppo,
di questo non potete fare il plot. Ovvero 

>	p:=taylor(exp(x),x=0,5): plot(p);

 

 

Warning, unable to evaluate the function to numeric values in the region; see the plotting command's help page to ensure the calling sequence is correct

 

per poterlo fare, occorre prima convertire lo sviluppo in polinomio (togliere l'O) e, se si desidera, far diventare il polinomio una funzione. 

>	p:=unapply(convert(p,polynom),x);

 

(2)

 

In questo esempio, spero di chiarire il risultato del comando unapply: 

>	f:=x->exp(x); q:=cos(x): q:=unapply(q,x);

 

 

	(3)

 

>	plot([f,p],-5..5);

 

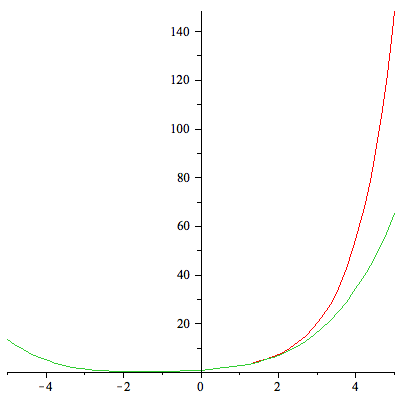ESERCIZIO: Disegnare il grafico di f(x)=cos(x) e dei suoi primi 10 polinomi di Taylor centrati nell'origine. 

====================================== 

Quanto è buona numericamente l'approssimazione? Dipende dal Teorema di Taylor+Lagrange: se f  è derivabile n volte con continuità e esiste la derivata di ordine n+1 in un intorno U di x_0, allora per ogni x  in U  esiste un punto t nell'intervallo di estremi x e x_0 tale che 

= 

Quindi: se abbiamo una buona stima delle derivate di f, possiamo: 

a) valutare l'errore che commettiamo approssimando f(x) con il suo polinomio di Taylor di ordine n 

b) determinare l'ordine di un polinomio di Taylor che approssimi la nostra funzione a meno    di un errore prefissato. 

ESERCIZIO: Approssimare il numero e a meno di 10^(-7). La velocità di convergenza è molto rapida, se confrontata col procedimento che avevamo visto a novembre (n=800 per avere due cifre decimali esatte). 

>

 

>	E:=10^(-7):   n:=1:    f:= x->exp(x):   r:=k->3/((k+1)!): while r(n)>E do n:=n+1: end do: s:=taylor(f(x),x=0,n+1); p:=unapply(convert(s,polynom),x); print('e'=p(1.));

 

 

 

	(4)

 

>	exp(1.)-p(1.);

 

(5)

 

>

 

ESERCIZIO: Approssimare sin(2) a meno di 10^(-6). 

>

 

=========================================== 

>	taylor(sin(x^(4/3)),x=0,2);

 

Error, does not have a taylor expansion, try series()

 

Spiegare la risposta di Maple. 

>

 

>